Failure isn’t an option, but it happens. Modeling the possibility that a portfolio strategy will stumble isn’t exactly cheery work, but it’s a productive and necessary exercise for stress testing what the future can do to the best-laid plans of mice and men. The good news is that there’s a rainbow of options for estimating the potential for trouble. But it’s usually best to start with a basic framework before venturing into more exotic realms.
A solid way to begin is by calculating the probability that a portfolio’s return will fall short of a particular benchmark or return. Larry Swedroe, director of research for the BAM Alliance, last month wrote about the probability of underperformance from the perspective of four factor premiums. The technique is to assume a normal distribution of returns and model the outcome under a variety of scenarios. Normal distributions are problematic, of course, due to fat-tail risk. But as Swedroe correctly points out, a normal distribution is “reasonable for multi-annual returns data because annual returns data is approximately normally distributed for diversified portfolio.”
The details for the number crunching are straightforward. Several years ago The Calculating Investor outlined the procedure with an Excel spreadsheet. Let’s expand the concept a bit by applying the normal distribution function in R via thepnorm() command.
Assume we’ve designed a portfolio with a 10-year time horizon and an expected annualized volatility (standard deviation) of 15%. Holding those variables constant, here’s the probability of generating a below-zero return over that span based on a range of expected returns:
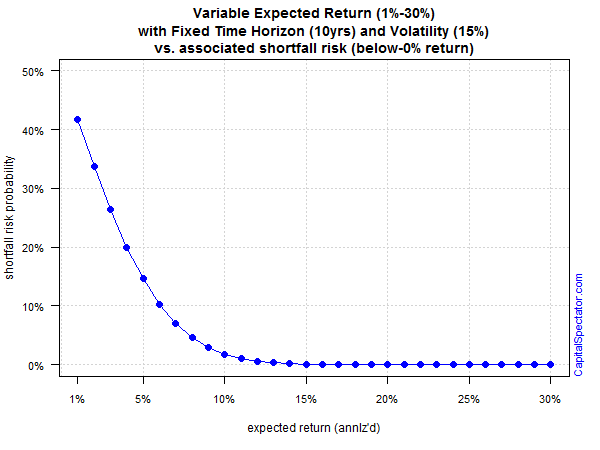
Not surprisingly, the risk of suffering a negative result is substantial if we’re assuming a low return. A 1% annualized return carries a 40%-plus risk a sub-zero performance over a 10-year stretch. But as expected return rises, the risk of below-zero performance falls. As the portfolio’s projected return approaches 10%, the risk of losing money fades to a virtually nil possibility.










Leave A Comment